传热学——热传导
基础概念
- 像重力场, 速度场一样, 物体中存在温度的场, 称为温度场(temperature filed), 它是各个时刻物体中各点温度所组成的集合, 又称为温度分布(temperature distribution)
- 温度场可以分为两大类:
- 稳态工作条件下的温度场
- 工作条件变动(即非稳态)的温度场
- 函数法描述:温度场是坐标与时间的函数 $$ t = f(x,y,z,\tau) $$ 稳态温度分布的表达式简化为 $$ t = (x,y,z) $$
- 图示法描述: 温度场中同一瞬间相同温度各点连成的面称为等温面(isothermal surface)
等温线的性质:
- 不可能相交
- 对连续介质, 其只可能在物体边界中断或完全封闭
- 沿线 (面) 无热量传递
- 由其疏密可直观反映不同区域温度梯度相对大小
- 温度变化最剧烈的方向为法线方向 n, 温度梯度 $grad t = \frac{\partial t} {\partial n}$
傅里叶定律
傅里叶导热定律的表达式在一维方向如下:
| 热流量 | 热流密度 |
|---|---|
| $\Phi =- \lambda A \frac{\partial t} {\partial x}$ | $q = -\lambda \frac{\partial t} {\partial x}$ |
式中, 符号代表传热方向指向温度降低的方向, 即热流方向, 热流方向与法线方向相反
傅里叶导热定律的文字表达是: 在导热过程中, 单位时间内通过给定截面的导热量, 正比于垂直该截面方向上的温度变化率和截面面积, 而热量传递的方向则与温度升高的方向相反。
导热系数 $\lambda$ 的定义式由傅里叶定律的数学表达式给出, 数值上, 它等于在单位温度梯度作用下物体内热流密度矢量的模 $$ \lambda = \frac{|q|} { | \frac{\partial t} {\partial n} n |} $$ 导热系数的数值取决于物质的种类和温度等因素, 一般地, 有如下规律:
- $\lambda$ 金属 > $\lambda$ 非金属
- $\lambda$ 固 > $\lambda$ 液 > $\lambda$ 气
常见物质的导热系数:
| 纯铜 | 碳钢 | 水 | 空气 |
|---|---|---|---|
| 398 W/(m·K) | 36.7 W/(m·K) | 0.599 W/(m·K) | 0.0259 W/(m·K) |
根据 08 年国标: 当 $\bar{t}$ ≤350°C 时, $\lambda$ ≤0.08 W/(m·K)的材料可用为保温材料
导热问题的数学描写
也即微分方程与定解条件的列写
导热微分方程
由能量平衡法 E 内增 = U 传入 -U传出+ $\Phi$ 自产热可知, 直角坐标系下导热的微分方程为 $$ \rho c \frac{\partial t} {\partial \tau} = \frac{\partial} {\partial x} (\lambda \frac{\partial t} {\partial x}) + \frac{\partial} {\partial y} (\lambda \frac{\partial t} {\partial y}) + \frac{\partial} {\partial z} (\lambda \frac{\partial t} {\partial z}) + \dot{\Phi} $$ 这是最基本的导热微分方程, 式中:
- $\rho c \frac{\partial t} {\partial \tau}$ 为非稳态项, 在稳态传热中为 0
- $\dot{\Phi}$ 为内热源项, 在无内热源的情况下为 0
- $\frac{\partial} {\partial x} (\lambda \frac{\partial t} {\partial x}) + \frac{\partial} {\partial y} (\lambda \frac{\partial t} {\partial y}) + \frac{\partial} {\partial z} (\lambda \frac{\partial t} {\partial z})$ 为各坐标方向净导入的热量
一些具体情况下的简化:
- 物性参数 $\lambda$ 为常数: $\rho c \frac{\partial t} {\partial \tau} = \lambda ( \frac{\partial ^2 t} {\partial x ^2} +\frac{\partial ^2 t} {\partial y ^2} +\frac{\partial ^2 t} {\partial z ^2}) + \dot{\Phi}$
- 物性参数 $\lambda$ 为常数且无内热源: $\rho c \frac{\partial t} {\partial \tau} = \lambda ( \frac{\partial ^2 t} {\partial x ^2} +\frac{\partial ^2 t} {\partial y ^2} +\frac{\partial ^2 t} {\partial z ^2})$
- 物性参数 $\lambda$ 为常数、无内热源的稳态导热 (拉普拉斯方程) : $\frac{\partial ^2 t} {\partial x ^2} +\frac{\partial ^2 t} {\partial y ^2} +\frac{\partial ^2 t} {\partial z ^2} = 0$
- 一维稳态含内热源导热 (泊松方程) : $\frac{\partial} {\partial x} (\lambda \frac{\partial t} {\partial x} ) + \dot{\Phi} = 0$
由于 圆柱坐标系 和 球坐标系 分析较为复杂, 在本科阶段可只记忆一维形式, 即 在圆柱坐标系下: $$ \rho c \frac{\partial t} {\partial \tau} = \frac {1} {r} \frac {\partial} {\partial r} (\lambda r \frac {\partial t} {\partial r} ) + \dot{\Phi} $$ 球坐标系下: $$ \rho c \frac{\partial t} {\partial \tau} = \frac {1} {r^2} \frac {\partial} {\partial r} (\lambda r^2 \frac {\partial t} {\partial r} ) + \dot{\Phi} $$
导温系数
将方程左侧的 $\rho c$ 移动至右侧与 $\lambda$ 组合可获得一个全新的物性参数: **热扩散系数 **a (导温系数), 其定义为: $$ a = \frac{\lambda} {\rho c} $$
- 分子: 导热能力与导温能力正相关
- 分母: 单位体积的物体每升高一度所需的热量
- 反映了物体在给定热量时温度升高的快慢、传热能力的大小——温度传播的快慢 辨析:
导热系数 $\lambda$ : 物体间接触时传热快慢 (即传递能力) 导温系数 $a$ : 物体内部热量传递快慢 (即补给能力)
定解条件
对于非稳态导热来说, 定解条件为 初始条件 加 边界条件 , 而对于稳态导热来说, 定解条件仅为 边界条件
常见的边界条件:
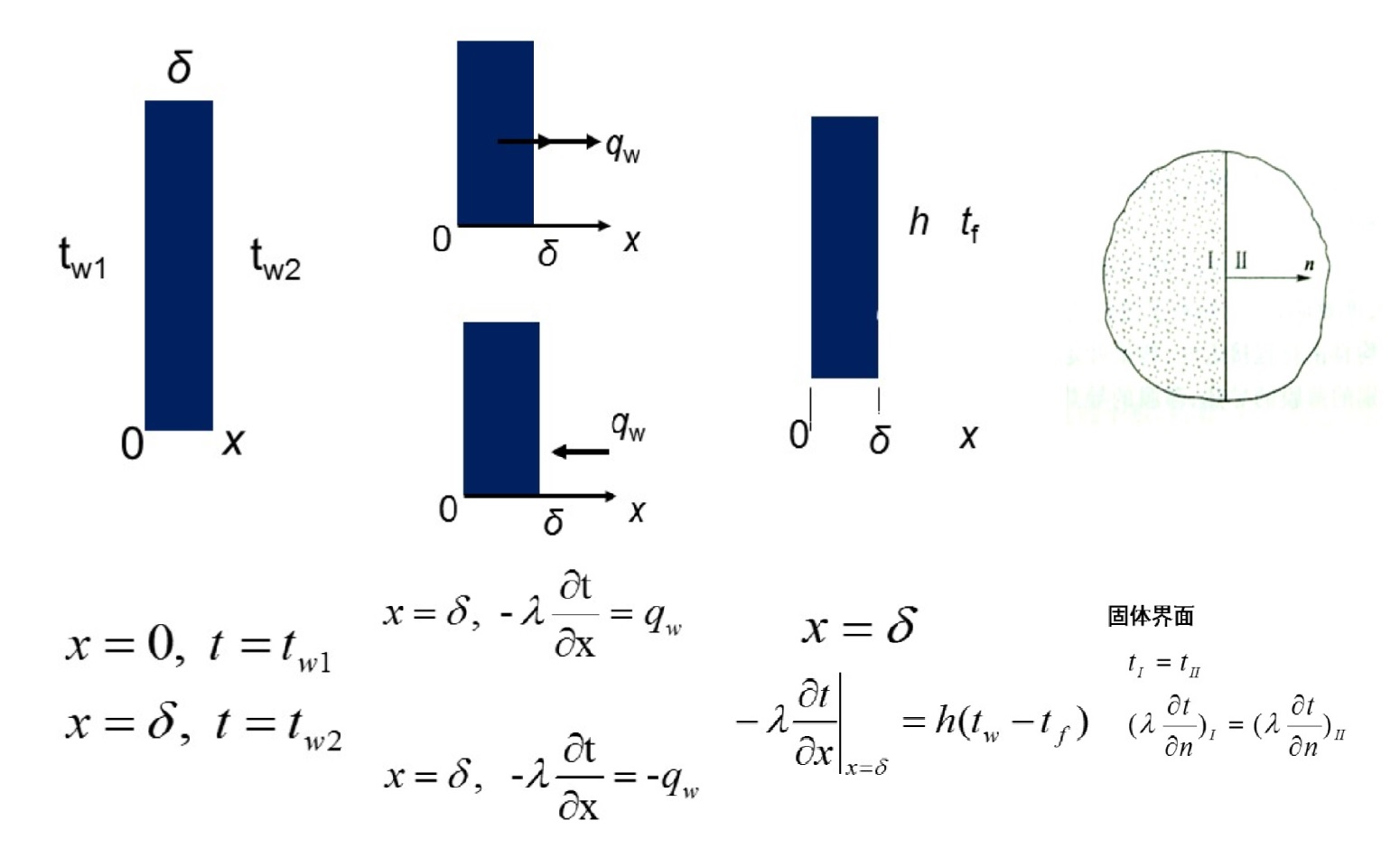
- 第一类边界条件: 指定边界上的温度分布
- 第二类边界条件: 给定边界上的热流密度
- 第三类边界条件: 给定边界面与流体间的换热系数和流体的温度, 也称为对流换热边界
- 辐射边界条件: 只发生辐射换热
- 固体界面边界条件 (也称第四类边界条件):tI = tII
上图中从左至右分别为第一到四类边界条件 辐射边界条件为 $- \lambda \frac{\partial T} {\partial n} = \varepsilon \sigma (T _\omega ^4 - T _e ^4)$
举例如下:
最终数学描述应该为微分方程+定解条件的形式, 并将定解条件代入可求得温度分布
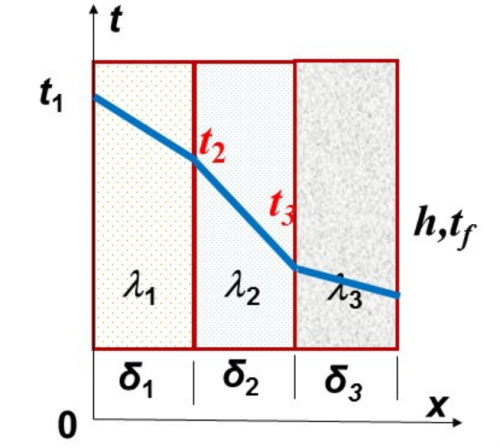
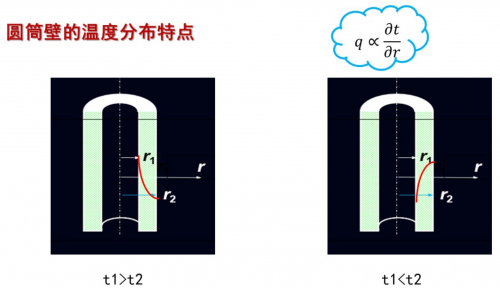
各种壁面的温度分布
技巧小结
- 求解温度分布、热流密度以及某界面温度 采取数学描述法
- 求解热流密度或某界面温度 采取热阻分析法更加简便
 高山流水觅土豆
高山流水觅土豆