传热学——热对流
工程中常见的还是利用对流换热,然而对流换热也是相对来说最复杂的一种换热,其涉及的变数也最多,对此将对流换热相关内容记录于此。
对流换热的分类
对流换热有较多的影响因素,首先便是有相变与无相变的区别。这两种换热的本质区别便是是否利用了工质的汽化潜热,同时外在表现就是在换热过程中工质的温度参数是否保持不变。 (插入相变)
在相变换热中,一般利用的方式有凝结换热和沸腾换热。很显然,凝结换热利用的是气态到液态、液态到固态相变过程放出的热量,而沸腾传热则更加类似于“烧水”过程,通过不断加热液体工质促进其沸腾,使整个容器内溶液受到巨大扰动,产生高强度的换热。
在无相变换热过程中,则可以分为受迫对流换热、自然对流换热以及混合对流换热。这里也很好理解,受迫对流就是通过一些人工的外力手段向流体施加外力导致其流动而形成的换热。自然对流则是源于自然现象,利用空气间温差形成的风等自然现象产生的对流而形成的换热。混合对流则是同时存在自然对流与强迫对流的情况,这种在生活中更加常见。
在强迫对流中还可简单分为内部流动和外部流动,而自然对流换热也可以简单分为无限空间与有限空间。
对流换热的无量纲准则数
对流换热中流体的流动状态对换热的效果影响较大,故需要确认流体的状态,为方便确认,引入了对无量纲准则数的使用。
| 无量纲数 | 缩写 | 物理意义 | 计算公式 | 备注 |
|---|---|---|---|---|
| 毕渥数 | Bi 数 | 固体内部导热热阻与界面换热热阻的相对大小 | $\frac{hl}{\lambda_s}$ | |
| 傅里叶数 | Fo 数 | 无量纲时间, 表征非稳态导热过程进行的深度 | $\frac{a \tau}{l}$ | |
| 努希尔特数 | Nu 数 | 壁面上流体的无量纲温度变化率 | $\frac{hl}{\lambda_f}$ | |
| 普朗克数 | Pr 数 | 动量扩散能力与热量扩散能力的相对大小 | $\frac{v}{a}$ | |
| 雷诺数 | Re 数 | 表征惯性力与粘性力的相对大小 | $\frac{ul}{v}$ | |
| 格拉晓夫数 | Gr 数 | 表征浮升力与粘性力的相对大小 | $\frac{g \alpha_V \Delta t l^3}{v^2}$ |
掌握这些无量纲准则数对掌握对流换热具有重大意义
强迫对流
如上所述,强迫对流分为内部和外部两种情况。我们可以简单的理解成:在管道内部流动的流体为内部流动,而采用流体外掠换热器件则为外部流动。
内部强制对流传热
内部流动对流传热速率方程如下:
$$ q_x = h_x( t_w - t_f )_x $$ 其中, $t_f$ 为流体截面平均温度。
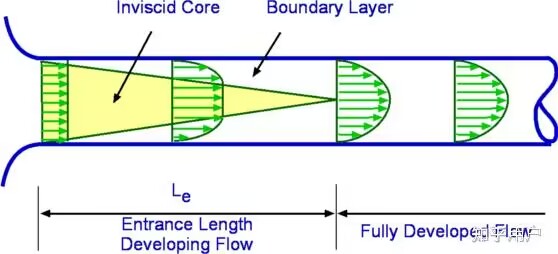
管内对流传热在边界层发展、速度分布、温度分布以及剪切力、摩擦系数、表面传热系数等方面均与外部传热存在显著不同。在管内的流动可以分为流动入口段和流动充分发展段,造成这种现象的实质是流动边界层受管内边界的限制。其流动状态可以凭借 Re 数进行判断,当采取 $Re=\frac{u_m d}{v}$ 一式进行判定时,其对应关系如下:
| 流动状态 | 判断 |
|---|---|
| 层流 | $Re \in [0,2300)$ |
| 过渡流 | $Re \in [2300,10000]$ |
| 旺盛湍流 | $Re \in [10000,\infty)$ |
流动入口的长度对于层流来说约为 0.05 个 Re,而对于湍流来说则≥10。当流动进入充分发展区后,其流动速度具有“自模化”的性质,其速度分布将自动定型。
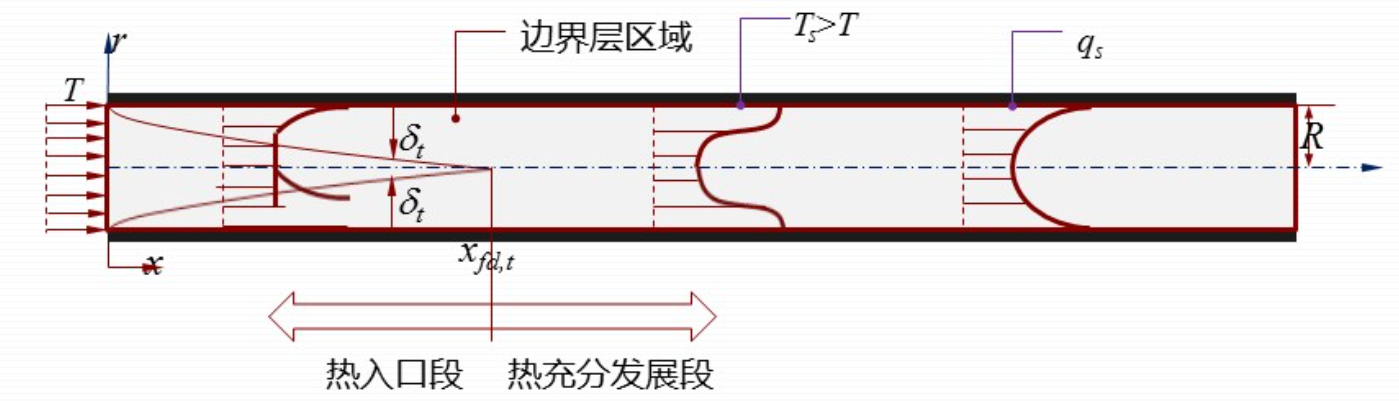
除去速度分布外,由于换热,其热量分布也需要研究。热入口段与流动入口段类似,当流体流态为层流时,热入口段长度约为 0.05 个 RePr,当其为湍流时则约为 10。在热充分发展区,工质性质不发生变化的情况下,也存在“自模化”的情况,其温度分布为:
$$ \frac{\partial{\Theta}}{\partial{x}}=0 $$ 其中,$\Theta = \frac{t-t_w^x}{t_f-t_w}$,$t_f$ 为截面的平均温度。
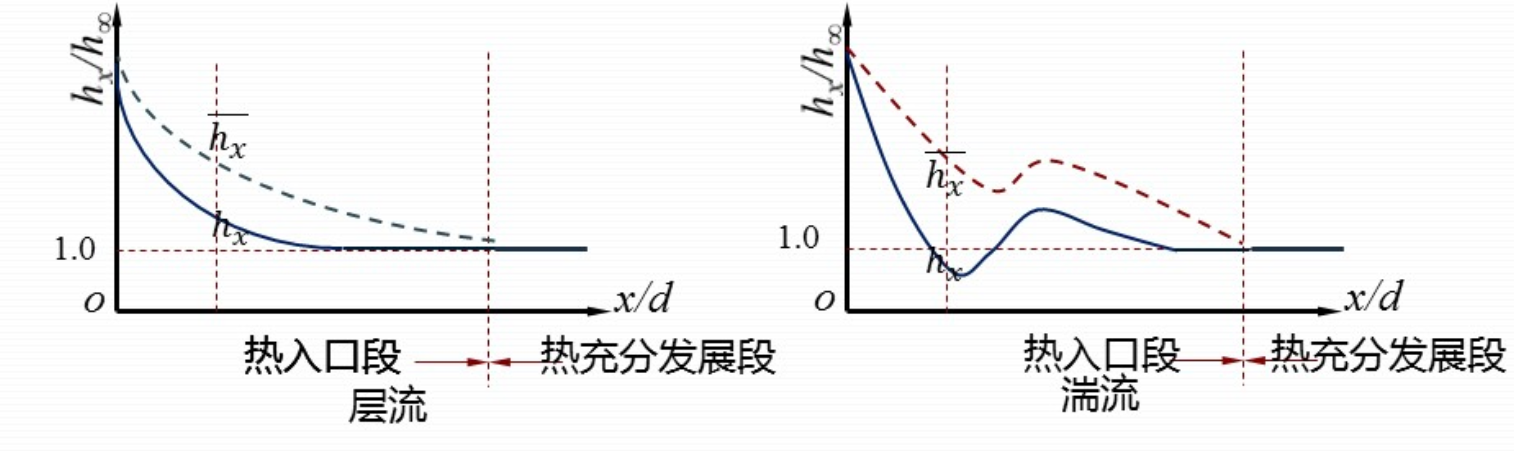
内部对流传热系数变化规律如图:
由图像可以分析出:
- 入口段换热能力较高。
- 对于常物性工质来说, 在热充分发展段 $h_x$ 可以视为常数。
 高山流水觅土豆
高山流水觅土豆