机械设计基础——平面机构的自由度和速度分析

绪论概念辨析

• 构件: 独立的运动单元
• 零件: 独立的制造单元
• 机构: 能够用来传递运动和力或改变运动形式的构件组合体
• 机器: 根据某种使用要求而设计的构件的组合体

运动副及其分类

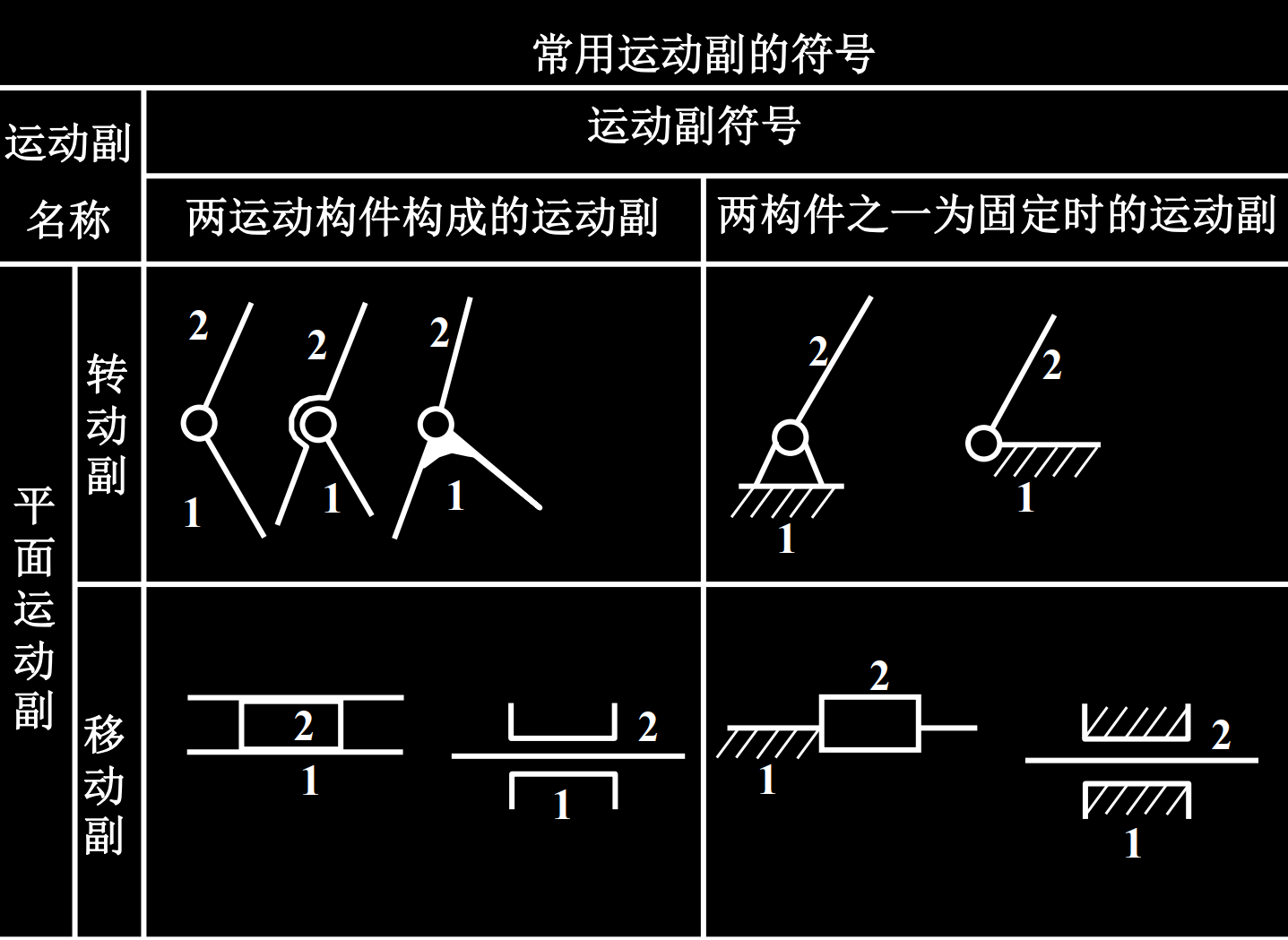
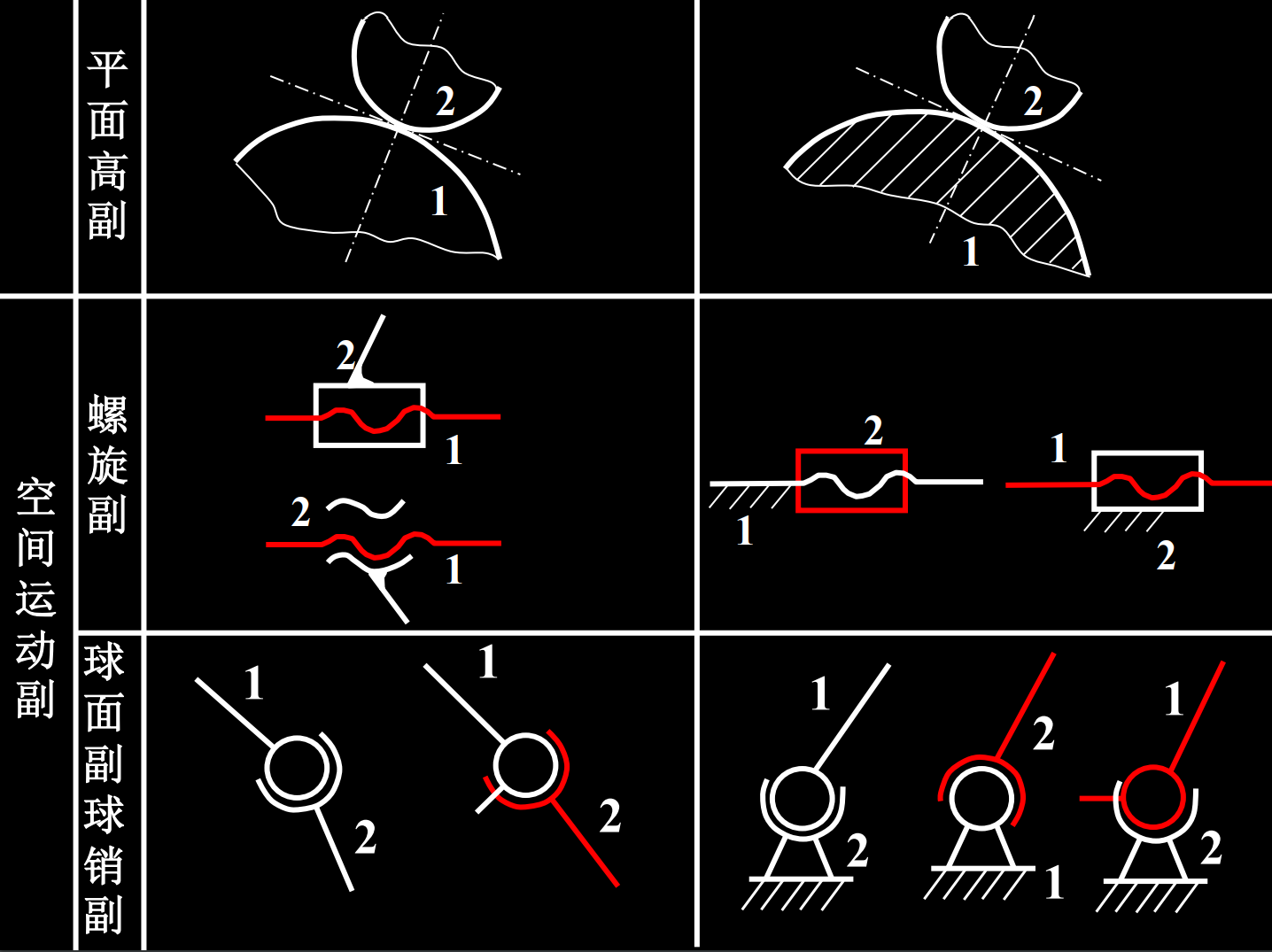
两构件组成运动副, 其运动副元素不外乎点、线、面。按照接触特性通常把运动副分成以下几类：

1. 低副——面接触，应力低

   • 转动副：若组成运动副的两构件只能在平面内相互转动，这种运动副称为转动副
   • 移动副：若组成运动副的两构件只能沿某一方向做相对对直线移动，这种运动副称为移动副

2. 高副——点、线接触，应力高 两构件通过点或线接触组成的运动副称为高副

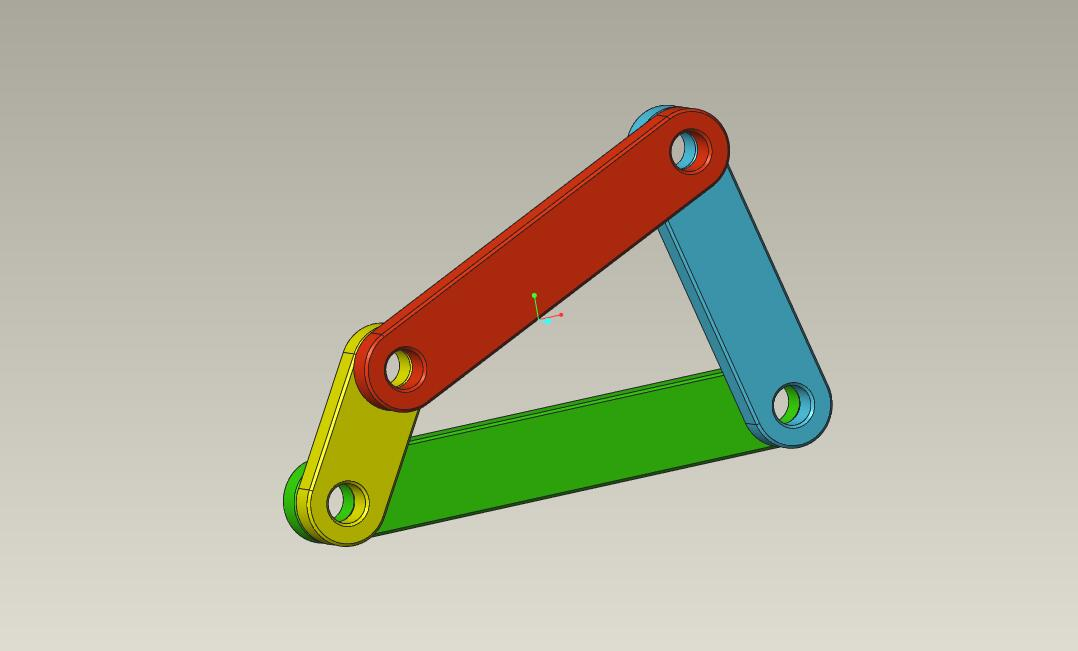
机构运动简图的绘制

绘制图示与注意

绘制步骤

机构中的构件可分为以下三类：

1. 固定构件（机架）：用来支承活动构件的构件
2. 原动件（主动件）：运动规律已知的活动构件
3. 从动件：机构中随原动件运动而运动的其他构件

画构件时应当撇开构件的实际外形，只考虑运动副的性质。

1. 确定构件数目
2. 确定运动副的种类和数目
3. 选定适当的比例尺
4. 将机架画上阴影线，并在原动件注明运动方向

平面机构的自由度

平面机构由 n 个活动构件构成（即除去机架），若机构中低副数量为 P_L个, 高副个数为 P_H个, 自由度为 F, 则 $$ F = 3n -2P_L -P_H $$ 其中应注意有复合铰链、虚约束、局部自由度的情况。

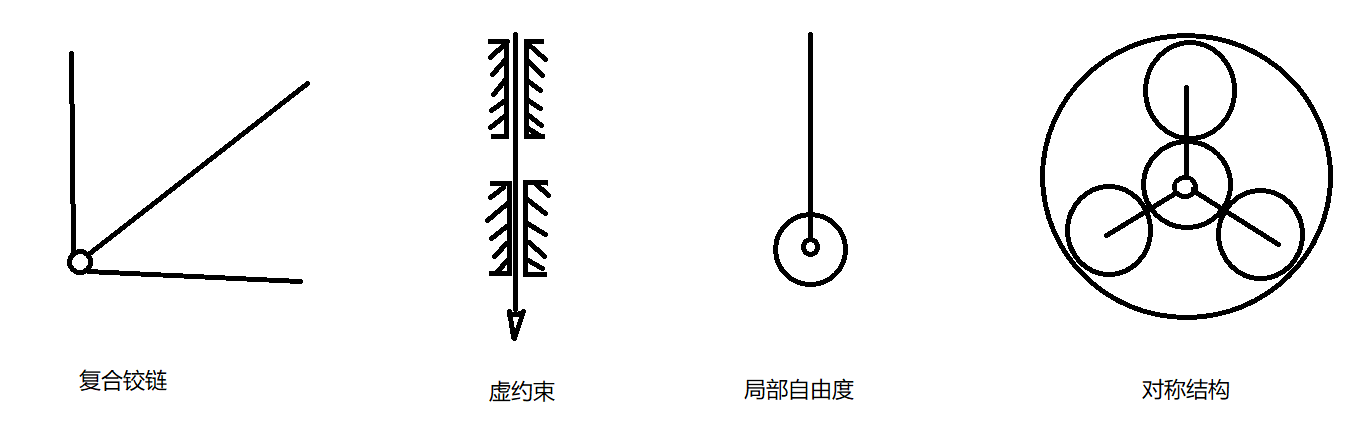
• 复合铰链下具有（N-1）个低副
• 对于那些不对构件运动造成影响的约束为虚约束, 应当忽视
• 对于可旋转滚子, 其转动副不影响确定运动, 却引入了一个自由度, 应去除这种局部自由度
• 对于对称结构 (如行星轮系)应只计算一个独立部分

  

速度的计算 (速度瞬心法)

瞬心的确定

相连构件的瞬心

在任一瞬时, 两构件间的相对运动可看做绕某一重合点的转动, 该重合点称为速度瞬心或瞬时回转中心, 简称瞬心。 如果这两个构件都在运动则称其瞬心为相对瞬心，如果两构件之一是静止的则称绝对瞬心。

• 所有机架与构件的瞬心均为绝对瞬心

瞬心的确定有以下几种情况：

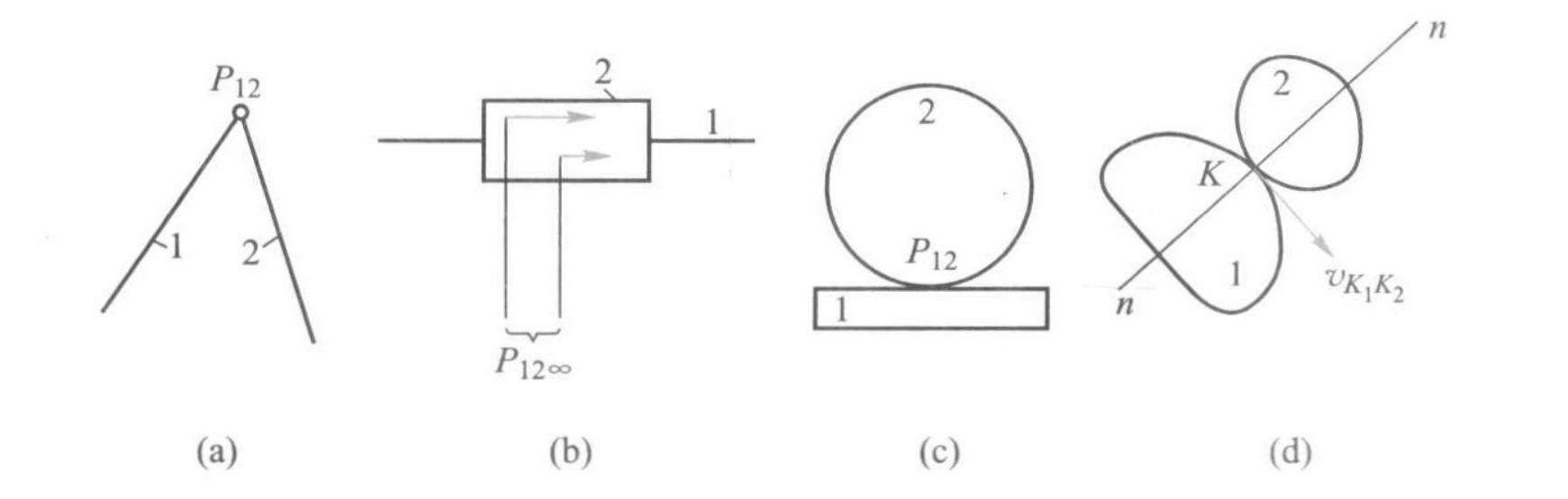
1. 两构件组成转动副时，转动副中心为其瞬心
2. 两构件组成移动副时，其瞬心位于移动导路垂线的无穷远处
3. 两构件组成纯滚动高副时，接触点就是其瞬心
4. 两构件组成滑动兼滚动的高副时，其瞬心位于过接触点的公法线 n-n 上，具体位置需要其他条件确定

   

三心定理

对于不直接接触的各个构件, 其瞬心可用三心定理寻求。即做相对平面运动的三个构件共有三个瞬心，这三个瞬心位于同一直线上

• 各构件间的联系可用画多边形的方法寻找，如： 若有一四杆机构标号为 1,2,3,4 首尾相连，则可抽象成一个正方形进行三心定理的求解

  

速度的求解

两构件的角速度与其绝对瞬心至相对瞬心的距离成反比。 设机架为 1 号构件，则 $$ \frac{\omega_i} {\omega_j} = \frac{P_{1j} P_{ij}} {P_{1i} P_{ij}} $$ 若求线速度只需使用 $$ v = \omega r $$ 其中, r 为求速度点到速度瞬心的距离。