热力学第二定律
由于热力发电厂课程的综合性,我需要重拾工程热力学等前置知识。恰好我在博客中记录的工程热力学相关内容还有一部分没有记录完整,借此机会也补充于此。
热力学第二定律
热力学第二定律
热力学第二定律的官方定义如下:
克劳修斯曰:“热不可能自发地、不付代价地从低温物体传至高温物体。”
开尔文曰:“不可能制造出从单一热源吸热,使之全部转换为功而不留下其他任何变化的热力发动机。”
这是热力学第二定律的学术说法,乍一看并不是很好理解。事实上,这句话在生活中可以举个例子进行理解,如不可能出现“一片湖面在自然状态下自己突然结冰而外部气温30℃”这种情况。也就是说,原本就冷的东西不可能自己就变得更冷,原来就热的东西不可能自己就变得更热,这段表述虽然不够严谨,比如说没有考虑到自发放热的化学反应使热的更热等现象,但是对于简单理解热力学第二定律还是十分直观形象的。
熵的导出
事实上,热能的微观表现即是分子的内能,其由分子的动能和分子间的势能组成。对于固体和液体这类不可压缩的物质,其温度的变化大多只与其分子内动能有关。而对于气体来说,分子间的势能也可能变化——即其温度可能与压强有关。
这里提到微观分子的原因是:热力学第二定律章节引入了熵的概念。熵的提出经历了一系列数学变换,其初始是根据热效率的概念所列出的一个等式。在任意卡诺循环中,定温吸热过程后,工质与热源温度都为$T_{r1}$,经过定温放热过程后,工质与冷源温度都是$T_{r2}$。设吸热过程中工质吸热为$\delta Q_1$,放热过程中工质放热为$\delta Q_2$,则根据卡诺循环热效率的表达式可以得到
$$ 1-\frac{\delta Q_2}{\delta Q_1}=1-\frac{T_{r2}}{T_{r1}} $$
使用代数值时,$\delta Q_2$为负值,在其前方加负号后经过简单化简可得到
$$ \frac{\delta Q_1}{T_{r1}}+\frac{\delta Q_2}{T_{r2}}=0 $$ 这就是熵这个状态参数导出的初始。后面要进行一系列的数学变换,感兴趣的我丢在下面,最后会得到这样一个式子:
令可逆绝热线数量趋向无穷大,任意两根可逆绝热线之间相距无穷小(这一步是将实际情况切分为无数个卡诺循环),则所有小循环都可用微元卡诺循环积分求和,即可得出
$$ \int_{1-A-2} \frac{\delta Q_1}{T_{r1}} + \int_{2-B-1} \frac{\delta Q_2}{T_{r2}} =0 $$ 式中的$\delta Q_1$与$\delta Q_2$都是工质与热源间的换热量,既然采用了代数值,则可以统一用$\delta Q_{rev}$表示。(注:这里指的是每一个微元可逆循环,既然是可逆循环,那么状态点就只有起点和终点,那么$\delta Q_1$就会和$\delta Q_2$数值上相同,仅有符号相反,后面的T也是如此) $T_{r1}$和$T_{r2}$是换热时的热源温度,统一用$T_r$表示。则上式可以改写为
$$ \oint\frac{\delta Q_{rev}}{T}=0 $$
总之最后得到了上面这个看着就很难的式子,不过别担心,我们先解释一下这个式子。
这个式子其所代表的意义为:任意工质经过任一可逆循环,微小量 $\frac{\delta Q_{rev}}{T}$ 沿循环的积分为零。上式的积分由克劳修斯首先提出,故称为克劳修斯积分。然后根据状态函数的数学特性,可以断定被积函数 $\frac{\delta Q_{rev}}{T}$ 是某个状态参数的全微分。1865年,克劳修斯将这个新的状态参数命名为熵。在我们实际的生产生活应用中,一般查询物性参数表来使用,不需要我们自己计算。但是这个定义式应当熟记,对于平均吸放热温度的计算具有妙用。
熵、㶲、𭴊
经过上面的步骤,我们了解到了熵这个物理量的前世,为了好好使用它,我们来看看它的今生。这玩意虽然有一个不好解释的原型公式,但是它自己也可以表示一定意义。熵的物理意义是体系混乱程度的度量。这个物理意义可以从微观内能的方面看得出:熵越大,微观粒子的混乱程度越大,即其无序性高,无序性高意味着其在每个时刻的下一刻可能出现的位置范围大,则意味着其内部分子内能中,势能含量小,动能的含量大。值得注意的是:熵是宏观量,谈论个别的微观粒子的熵是没有意义的。
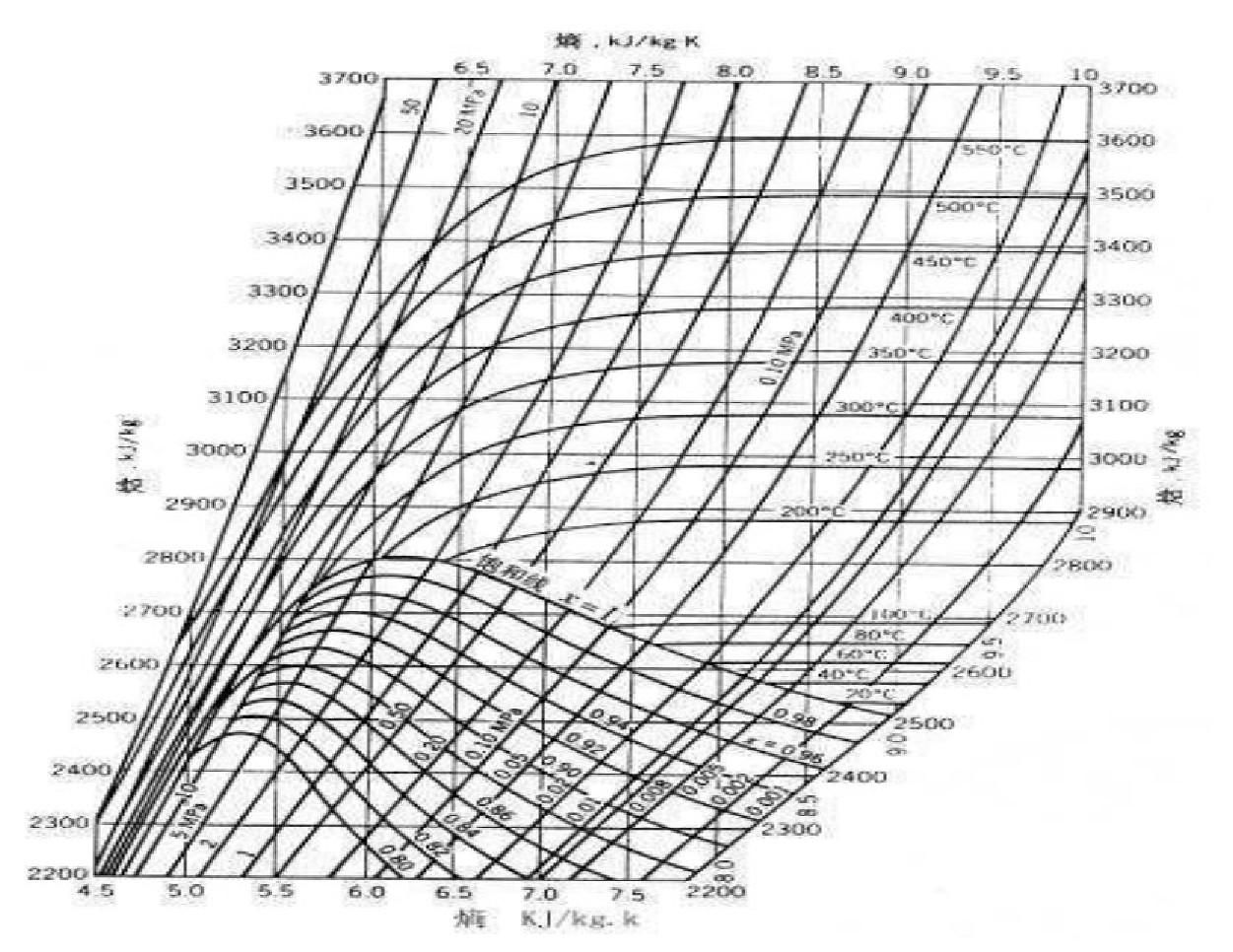
在使用这个物理量时,我们通常搭配 T-S 图(即温熵图)或 h-s 图(即焓熵图)食用,根据前面热力学第一定律相关内容我们可以知道,在压力一定的情况下,同一工质温度和焓是一一对应的关系。
事实上,熵这个物理量一般用于表征物体的做功能力,由于熵增原理,孤立系统总是向无序方向发展,比如一瓶压缩后的气体,其向无序方向发展的结果便是膨胀到与环境一致。膨胀必然伴随着做功过程,以此我们可以大致的理解为什么熵可以表征做功能力。
经过大量的实践证明,各种形态的能量相互转化时,具有明显的方向性。如机械能、电能等就可以全部转化成热能,理论上转换效率可达100%。这类可以无限转换的能量称之为㶲,由于机械能全部为㶲,故习惯上将有用功作为无限可转换的能量的同义词。但是反方向来说,热能转化为机械能、电能等,不可能全部转化,转换能力受到热力学第二定律的制约。故从技术使用和经济价值角度来说,前者品位(或者说质量)更高,更加宝贵。而热能本身也分高低贵贱,举例来说,当热量从高温热源传向低温热源时可以通过可逆机作出有用功(如热力发电厂),从低温热源传向高温热源也可做功(如冰箱),但是地球表面上广泛分布的大气、海水等蕴含着丰富的热力学能,由于单一热源无法持续做功,因而它们提供的热量无法成为机械功,从动力观点称其为废热,或者是𭴊。故任何能量都是由㶲和𭴊组成,即
$$ E = E_x + A_n $$
热力循环
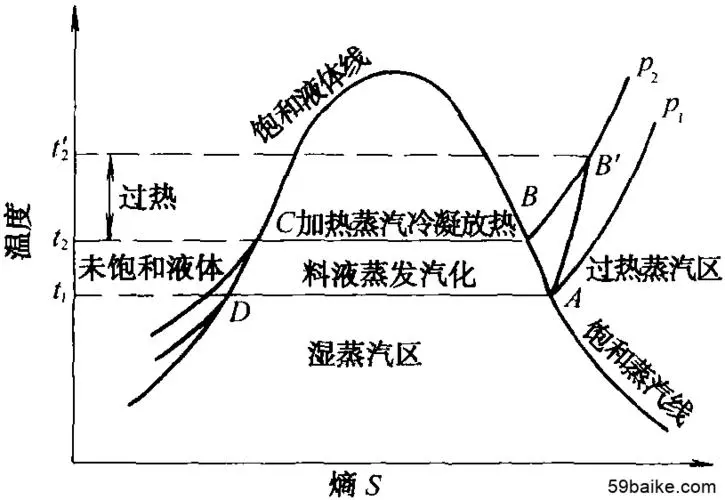
在实际生产生活中,我们一般利用的是各种热力循环达成各种目的,上方机械式蒸汽再压缩蒸发器工作循环的温熵图就是一个例子。我们常讲的热力循环有卡诺循环、奥托循环、狄塞尔循环、布雷顿循环、朗肯循环等。这里主要介绍我平时接触较多的卡诺循环和朗肯循环。
卡诺循环
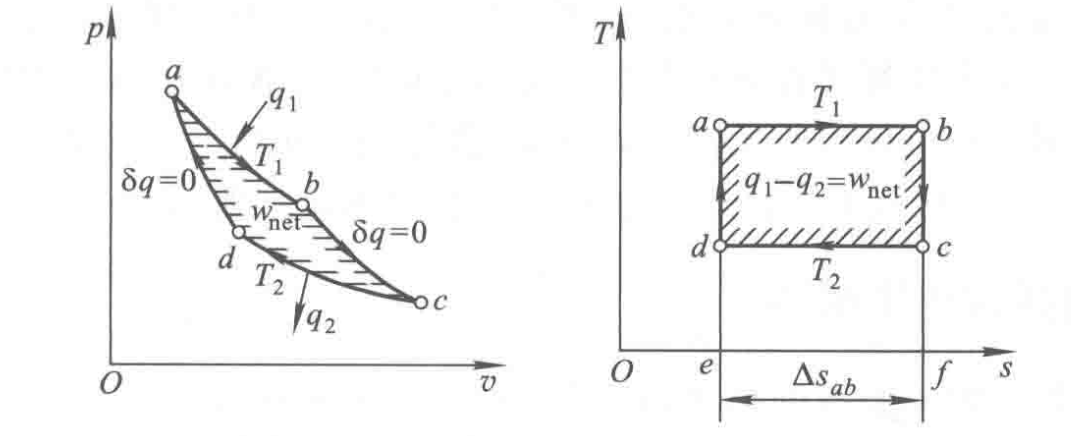
卡诺循环是热力学中的一个基本循环,由两个等温过程和两个绝热过程组成。其热力过程图如下所示:
卡诺循环描述了理想条件下热机的工作过程,包括从高温热源吸收热量、向低温热源放热、膨胀做功和压缩。这里我们对卡诺循环进行分析:
根据定义可知:循环热效率为
$$ \eta_t = \frac{w_{net}}{q_1} = \frac{q_1-q_2}{q_1} = 1 - \frac{q_2}{q_1} $$
由于卡诺循环包含两个绝对理想的绝热过程,这两个过程的换热量$\delta q$为0。由于整体可以构成一个闭合循环,故循环效率仅与剩下两段吸放热有关。 这里依旧是便于理解进行说明,可以选择跳过。
此处由于严格等熵,则$s_a=s_d$,$s_b=s_c$。因此我们可以得到$\Delta s_{a-b}=\Delta s_{d-c}=-\Delta s_{c-d}$。
由熵的定义可以反推出,整个过程的吸热量$q=\Delta s \cdot T$。这里为了便捷,取绝对值进行计算,并且将本是负值的熵的结果按照放热描述去掉负号,最终我们便可以得到
$$ \eta_t =1 - \frac{q_2}{q_1}=1- \frac{\Delta s_{c-d} \cdot T_2}{\Delta s_{a-b} \cdot T_1} = 1-\frac{T_2}{T_1} $$
最终我们可以知道,卡诺循环的热效率为 $$ \eta_t = 1-\frac{T_2}{T_1} $$
对此进行分析我们可以得到三点结论:
- 卡诺循环的热效率仅仅取决于高温和低温热源的温度。
- 卡诺循环的热效率只可能小于1,因为$T_1=\infty$或者$T_2=0$绝不可能达到。(这里指开氏温标)
- 当$T_1=T_2$时,循环热效率才为0。这表明,在温度平衡的体系中热能不可能转化成机械能,热能产生动力一定要有温度差作为热力学条件,从而验证了借助单一热源连续做功的机器是制造不出的,或者说第二类永动机是不存在的。
虽然至今未能制造出严格按照卡诺循环工作的热力发动机,但是卡诺循环是实现热机选用循环时的最高理想。
朗肯循环
朗肯循环是在热电等方面使用最多的循环,根据工程热力学书中所言,选用其作为基础理由如下:
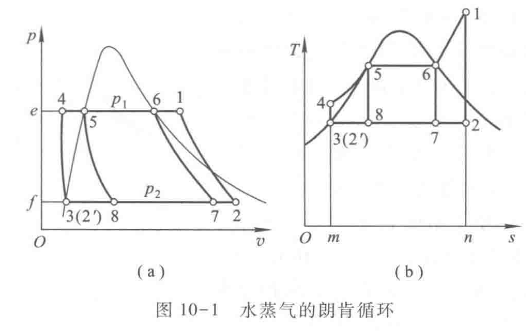
热力学第二定律指出在相同温限内,卡诺循环的热效率最高。在采用气体作工质的循环中,因定温加热和放热难以实施,而且在p-v图上气体的定温线和绝热线的斜率相差不多,以致卡诺循环的净功并不大,故在实际上难于采用。 在采用蒸汽作工质时,压力不变时液体的汽化和蒸汽的凝结的温度也不变,因而也就有了定温加热和放热的可能。更因这时定温过程亦即定压过程,在p-v图上与绝热线之间的斜率相差亦大,故所作的净功也较大。所以,以蒸汽为工质时原则上可以采用卡诺循环,如图10-1中循环6-7-8-5-6所示。然而在实际的蒸汽动力装置中并不采用卡诺循环,其主要原因是:首先在压缩机中绝热压缩过程8-5难于实现,因状态8是水和蒸汽的混合物,压缩过程中压缩机工作不稳定;同时状态8的比体积比水的比体积大得多,需用比水泵大得多的压缩机。其次,循环局限于饱和区,上限温度受制于临界温度,故即使实现卡诺循环,其热效率也不高。再次,膨胀末期,湿蒸汽干度过小,即含水分甚多,不利于动力机安全。实际蒸汽动力循环均以朗肯循环为其基础。

水蒸气的朗肯循环
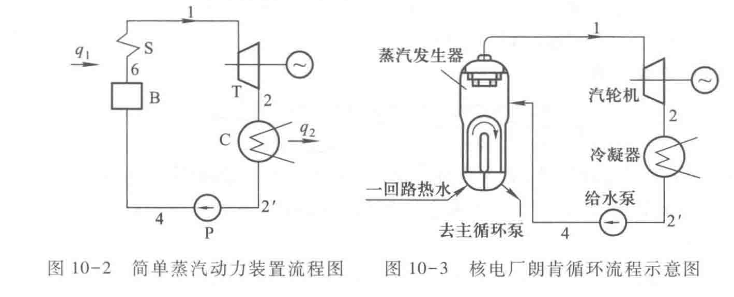
在实际应用中由于本人专业对于热力发电厂等应用更为接近,故在此仅根据下图进行电厂中的分析。我们认识到,在热力发电厂中,整体的汽水过程是是这样的:首先由锅炉或者蒸汽发生器 B 进行对工质或者说水的加热,在朗肯循环图中也就是 3-4-5-6-1 的过程。在这里,液态水被逐渐加热至气态,并成为过热蒸汽,其一共经历了“饱和液-气液混合态-饱和蒸汽-过热蒸汽”四个状态的转变。之后是膨胀做功部分,过热蒸汽凭借其高压力推动汽轮机 T 做功使其叶轮旋转,在汽轮机后接入发电机 G 即可发电。这部分为图上的 1-2 的过程,即近似的绝热膨胀过程。值得一提的是,终参数 2 点的干度十分重要,干度过低可能会影响设备的安全运行,故有些时候也在 1-2 过程途中加入再热环节以提高乏气干度。做功之后的乏汽进入冷凝器 C 放热成为冷凝水,完成的是 2-3 的过程。最后由给水泵将循环水打回锅炉 B 中。当然这是一个简化的循环,实际上我们还有更多的汽水辅助设备参与生产。
在这里,比较重要的几个公式便是循环效率,汽耗率等。仅贴几个公式在这里以备查用。 $$ \eta = \frac{h_1-h_2}{h_1-h_4} $$ 汽耗率 $$ g = \frac{3600}{h_1-h_2} $$
 高山流水觅土豆
高山流水觅土豆